Liutprand - Associazione Culturale

Sir William Flinders Petrie conobbe l’Egitto nel 1880 e trascorse la maggior parte di quello stesso anno eseguendo un rilievo molto esauriente delle piramidi dell’altopiano di Giza. Le sue misure molto attente della Grande Piramide, così come quelle intraprese per le piramidi di Chefren e Micerino, rimangono ancora l’opera definitiva e la massima autorità in materia. Le sue scoperte furono poi pubblicate nell’opera The Pyramids and Temples of Gizeh, 1883.

Petrie misurò l’altezza di ognuno dei 203 corsi (strati di pietre) della Grande Piramide. Poiché le pietre lisce dell’involucro esterno sono state quasi completamente saccheggiate e utilizzate per altri edifici, già da diversi secoli, oggi sono esposti i blocchi nel nucleo, o parte interna. I ricercatori come Petrie possono, quindi, salire sui gradoni della piramide, uno strato dopo l’altro, e, con l’utilizzo di un teodolite, prendere misure molto precise per ogni livello. Il metodo di Petrie è stato quello di misurare tutte le altezze su un lato della piramide, poi a ritroso, per tutto il percorso, lungo il lato opposto.

Ci si potrebbe aspettare che ciascuno strato di blocchi del nucleo abbia la stessa altezza, in modo regolare, ma non è così. Appare molto evidente che l’intenzione originaria era di progettare per ogni livello un’altezza diversa, che può variare da un minimo di 50 a un massimo di 150 cm.

Un altro punto interessante riguarda le altezze degli strati corrispondono a valori abbastanza astratti. Anche se le misure generali e gli angoli utilizzati per la costruzione della Grande Piramide sono riconoscibili, in quanto le stesse norme sono state utilizzate da molte altre civiltà cugine, le altezze dei livelli più alti sfuggono ad un riconoscimento. Perché mai?

Altezze inconsuete degli strati

Dal momento che la costruzione è stata fatta come un campionamento di misure, la Grande Piramide è stata molto attentamente progettata per incorporare importanti principi geometrici in tutte le sue caratteristiche esterne. L’angolo di pendenza è stato fissato a 51,84 gradi e la lunghezza del lato di base è di 230,43 metri. Progettata come una piramide tronca, con una cima piana quadrata che reggeva un altare, col lato di 13,40 m, c’era anche un codice verticale per l’altezza, che doveva essere mantenuto con una notevole precisione. L’unico modo per mantenere la precisione richiesta era di avere misure molto riconoscibili nel salire in pendenza, lungo la faccia inclinata, percorrendo il rivestimento in pietra. Utilizzando la trigonometria e misurando le altezze sia della faccia del blocco di rivestimento, sia quella della pietra del nucleo, con i rispettivi aumenti d’altezza da un livello all’altro, si sarebbe potuto determinare quando fosse stata raggiunta la misura corretta della faccia della piramide, di stazione in stazione.

Mantenere la precisione della fronte esterna, misurando verso l’alto lunghezze inclinate, era la conseguenza diretta del mantenere l’altezza corretta di ciascuno strato. Quindi, sommando tutte le misure delle altezze dei blocchi, poteva essere ben noto come l’edificio stava progredendo. Per fortuna, un corso di pietre del rivestimento è sopravvissuto, sepolto nella sabbia alla base della Grande Piramide, e ci può rivelare molto sulle caratteristiche di progettazione delle pietre del rivestimento su altri livelli, salendo lungo la piramide.

Ma perché tutti i livelli variano in altezza a tal punto?

La risposta sembra essere adeguatamente fornita dal Prof. Joseph Davidovits, scopritore del fatto che le pietre del rivestimento esterno e gli elementi del nucleo, dietro di loro, erano fatti in un’antica gettata di calcestruzzo (pietra artificiale):

‘Prima di costruire la prima piramide in pietra, gli antichi egizi costruirono monumenti molto imponenti di mattoni crudi. Troviamo grandi recinti di templio funerari della seconda dinastia, come quello di Khasekhemwy (2730 a.C.). Il suo muraglione è fatto di mattoni d’argilla cruda, quindi in un materiale realizzato con stampi. Si pensa generalmente, dato che questi mattoni sono stati realizzati in stampi, che la loro dimensione deve essere uniforme. Tuttavia, questo è sbagliato. Nonostante siano stati prodotti in stampi, i mattoni sono di almeno cinque formati diversi, il che implica l’uso di stampi diversi. Troviamo queste differenze nelle proporzioni in tutte le piramidi. Questa eterogeneità offre ai monumenti la capacità di resistere ai terremoti, evitando l’amplificazione delle onde sismiche’. Vedi: Joseph Davidovits, Why the pharaohs built the Pyramids with fake stones, Geopolymer Institute, Trad. ital.: Il calcestruzzo dei Faraoni, ed. Mondo ignoto, Roma, 2004.

Il corso inferiore della Grande Piramide è il più alto di tutti. La lunghezza misurata della superficie esterna in pendenza del corso di pietre di rivestimento della base è di 1,90 m, mentre l’altezza posteriore verticale raggiunge quasi 1,50 m. A causa di alcuni spostamenti della linea che separa i blocchi posteriori e centrali da quelli del rivestimento esterno, vi sono state variazioni nelle misure tra le pietre del rivestimento frontale e quelle poste dietro. Queste variazioni nella parte posteriore non aveva importanza, perché le pietre; rifinite con estrema precisione, servivano da telaio, così come i blocchi un po’ più ruvida core subito dietro, sono stati tutti realizzati in antico calcestruzzo, prima impastato e poi gettato in opera. Dietro, i blocchi del nucleo sono più rozzi, in parte estratti dalle cave di pietra e in parte gettati con aggregato di pietre di cava scheggiate.

La pietra della fotografia aveva una lunghezza misurata di 2,06 m lungo la faccia esterna. Questo darebbe una superficie di 3,918 metri quadrati, equivalenti a 6075 pollici quadrati (un codice lunare forte).

Basandoci su un rilievo topografico in scala di 5 pietre (con la scala in piedi egizi indicata), fornito in Great Pyramid in Fact and Theory, le lunghezze delle pietre adiacenti erano probabilmente di 1,42 m, 1,46 m, 2,23 m e 1,33 m, rispettivamente.

Queste lunghezze avrebbe fornito le seguenti superfici, in pollici quadrati: 4200 (forte codice di navigazione e lunare); 4320 (navigazione); 6.600 (navigazione,usando il miglio corrispondente a 5280 piedi); 3937,5 (forte codice di navigazione e lunare).

Nonostante l’apparente finitura levigata e buona miscelazione delle pietre di rivestimento e l’altezza uniforme delle facce esterne per ogni livello, si può tranquillamente ipotizzare che ognuno fosse di dimensioni diverse in lunghezza, rispetto ai suoi immediati vicini. È evidente che nulla potesse essere arbitrario e che le dimensioni delle facce, praticamente di ogni pietra, contenessero un elemento simbolico nei numeri di lunghezza, altezza e supeficie, misurati in pollici.

Il dimensionamento delle misure diagonali delle pietre esterne, livello per livello

Ci sono, come si è detto, 203 livelli, che furono misurati da Petrie, e di questi i primi due lo furono solo parzialmente, ma in modo sufficiente per conoscere le loro altezze reali, o di progetto. In tutta la storia documentata, non è mai stata documentata una cima appuntita per la Grande Piramide. Appare invece evidente che questa piramide particolare fosse progettata con la cima tronca, con una piattaforma per un altare o osservatorio sulla sua cima. In termini di codifica matematica, il valore d’altezza fornito dal livello 203 (453,6’ = 138,23 m) è perfetto per un tutorial in navigazione relativo alla circonferenza equatoriale della Terra.

Secondo le misurazioni accurate fornite da Petrie, il corso di pietre n.203, rado e mescolato (in alto), raggiunge un’altezza di 5451,8”, che è meno di un pollice più alto di 453,6’. C’erano almeno 3 valori di prossimità (due mnemonico ed uno letterale) che i matematici antichi avrebbero potuto voler leggere nell’altezza finita (a seconda di quale sistema di navigazione fosse stato inuso e del modo di effettuare il calcolo). I valori sono 453,6’, 453,75’ e 456,192’ (456 e 24/ 125).

Trentacinque corsi

Saliamo la piramide a un ritmo di 7 corsi per volta, sino al livello 35. Il livello numero 35 era alto quasi il doppio del corso che lo precedeva e, apparentemente, costituiva una tappa importante di messa a punto, prima di iniziare il corso successivo. Il raggruppamento di 35 corsi per raggiungere questo scopo era in linea con il sistema del calendario lunisolare e sabbatico, che operava in base al numero sette (Nota: 35 è 70 ÷ 2 o 7 x 5).

In base al sistema sabbatico, al termine del settimo anno sabbatico tutto doveva essere perfezionato e corretto prima di iniziare un altro ciclo di sette anni di calendario. Potremmo ancora scoprire che ci siano multipli di questi punti "pietre miliari" verso l’alto della piramide e che ognuno abbia una relazione con il numero sette. Passiamo ora ad avviare il processo di retro–ingegneria di 35 pietre – telaio per vedere se siamo in grado di elaborare la lunghezza diagonale necessaria per la faccia di ciascuna, in base alle misurazioni dei livelli fornite da Petrie. Per diversi motivi legati all’antica matematica e alla scienza dei sistemi di codifica, è abbastanza evidente che l’angolo di pendenza progettato della Grande Piramide fosse di 51,84 gradi (51° 50’ 24"). I diversi calcoli effettuati da Petrie, per determinare l’angolo progettato di pendenza di una costruzione molto corrosa dal tempo, si avvicinavano a questo valore altamente probabile e nella sua sintesi egli dichiarava: Tutto sommato, probabilmente non può fare di meglio che prendere 51º 52’ ±2’ come l’approssimazione più vicina all’angolo medio della Piramide, che consente di dare un certo peso al lato sud.

Vediamo i primi sette corsi:

1. Petrie determinò che questo livello di base fosse alto 58,6" sul lato NE, ma 57,6" su quello SW, con una differenza di un pollice in tutta l’estensione di base di circa 13 acri.

Un certo numero di blocchi dell’involucro esterno è sopravvissuto sotto la sabbia a questo livello e la loro lunghezza diagonale sulla faccia esterna è stata misurata in da 75".

Basandosi su anni di esperienza di costruzione, questo ricercatore presume che i blocchi di rivestimento dovessero raggiungere un livello leggermente superiore rispetto ai blocchi di base dietro di loro. La ricostruzione relativa all’altezza verticale di questo insieme di base di pietre involucro è 75" x sen 51,84° = 58,972" (58 243/ 250).

Ciò significa che il livello perfettamente orizzontale dei blocchi dell’involucro esterno si assestava circa 1/ 3 di pollice (un cm) al di sopra dei blocchi posteriori del nucleo, sul lato NE, e saliva sino ad essere 11/ 3 pollici (3,5 cm) più elevato sul lato SW. Questa leggera discrepanza nel livello perimetrale può essere rettificata, versando una miscela di malta di calcestruzzo che riempia le depressioni irregolari del nucleo centrale, per livellare tutto alla perfezione prima d’iniziare a costruire il corso successivo. Come ogni costruttore sa, è essenziale basarsi su un fondamento perfettamente livellato e squadrato, o si rischierebbe d’incontrare problemi a ciascuna fase di costruzione, sino al tetto. Come si è visto, ci sono voluti per i costruttori della Grande Piramide pochi corsi di rettifiche di poter finalmente realizzare qualcosa alla perfezione e chiudere il corso 4.

Basandoci sul disegno di Petrie dei blocchi del nucleo ad ogni livello e in che modo le pietre del rivestimento avrebbe interagito con loro, una vista laterale di una base tipica, usata come cassaforma esterna in pietra, potrebbe essere come questa:

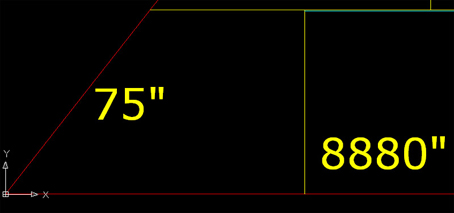
La diagonale della faccia misura 75". Idealmente, la lunghezza di base per i blocchi interni, dietro il rivestimento, doveva essere di 96", ma ciò varia a seconda delle irregolarità nei confronti del nucleo centrale dietro. L’altezza posteriore era di 58,972" e la parte superiore del blocco era lunga poco meno di 50", che a sua volta può variare a seconda di come si appoggiava la faccia del blocco centrale dietro. Dato che il nucleo posteriore centrale e le pietre stesse di rivestimento erano impastate con calcestruzzo, gettato e compresso in opera, piccole irregolarità nel supporto di base non avevano importanza, perché tutte le fessure, le tasche o fessure si riempivano, e poi venivano lasciate indurire alla perfezione. Una distanza di 8880" (740’ = 225,55 m) si stendeva fra i bordi posteriori delle pietre di rivestimento su entrambi i lati del sito e i costruttori avrebbero versato i blocchi di base all’interno di tale perimetro (su una superficie di oltre 5 ha).

Una sottile linea blu che interseca la linea gialla che la parte superiore del corso involucro di pietra. Questo rappresenta l’altezza misurata dei blocchi di base, che giacevano dietro le pietre di casseratura.

2. Petrie ha determinato che questo livello era alto 49,1" sul lato NE e 52,5" sul lato SW. Dunque i costruttori hanno cercato di compensare il piccolo errore del primo corso, che era fuori livello di 1" e inclinato verso SW. La seconda pietra dell’involucro intorno alla piramide ha una faccia inclinata lunga 65". La formula utilizzata è stata 65" x sen 51,84° = 51,10875". Sul lato SW della piramide la parte superiore del nucleo di pietra si assesta quasi perfettamente a livello con il blocco centrale dietro (il nucleo è 1/ 42 di pollice, ossia 0,6 mm, più alto). Sul lato NE, tuttavia, il rivestimento in pietra si trova più alto quasi 2,4 pollici del blocco centrale dietro e ci sarà stato bisogno di riempire con malta per stabilire un livello perfetto sopra il blocco del nucleo centrale. L’altezza delle pietre di rivestimento ha ora raggiunto 140" (35,56 m). I blocchi di questo secondo livello sono stati gettati all’interno di un perimetro quadrato con il lato di 8800" (733.3333’ = 223,52 m).

3. Petrie ha stabilito che questo livello 3 s’innalzava 48,2" sul lato NE e 45,3" sul lato SW. Ancora una volta i costruttori sembrano cercare di porre rimedio a un dislivello globale che favorisce il lato SW sul livello sottostante. La superficie esterna inclinata dei blocchi di rivestimento per questo livello è lunga 60". L’effetto è ora che la cima del rivestimento in pietra si trova a poco più di un centimetro più in alto dei blocchi interni sul lato NE e un po’ più di due centimetri al di sopra sul lato SW. L’altezza delle pietre di rivestimento ha ormai raggiunto 200" (50,80 m) e tutto è quasi perfettamente orizzontale, su tutta la superficie di questo livello. Gli elementi fondamentali di questo livello sono gettati all’interno di un perimetro quadrato, del lato di 8.700" (725’ = 221 m).

4. Petrie ha stabilito che questo livello 4 si elevava di 44" sul lato NE e 44,5" sul lato SW. Al fine di equilibrare quanto rimaneva dell’errore (1/2", circa un cm, a favore del lato NE), i costruttori fanno più alto il lato SW di 1/2". Il risultato è un livello quasi perfettamente orizzontale, con il lato SW solo 1/69 di pollice più alto (0,4 mm). I costruttori impastano e versano il calcestruzzo in un telaio di pietre, in modo che le facce esterne sono lunghe 56" lunghe e ora le pietre dell’involucro esterno si trovano leggermente al di sopra (1/ 2 pollice) rispetto ai blocchi del nucleo interno. La lunghezza diagonale delle pietre del rivestimento raggiungeva i 256". La formula per l’altezza del nuovo livello è 56" x sen 51,84° = 44,03125". Il livello 4 si trova all’interno di un perimetro quadratodi 8.640" quadrato (720’ = 219,46 m).

5. Petrie ha stabilito che questo livello 5 si alzava di 40,2" sul lato NE e 38,9" sul lato SW. Dopo aver raggiunto la perfezione virtuale del livello del livello 4, il lato NE si trova ora di poco più di un centimetro più alto sul lato SW.

Sembra plausibile supporre che la lunghezza diagonale lunghezza della faccia di questa serie di pietre fosse di 50". La formula è: 50" x sen 51,84° = 39,3144" (intesa come aumento verticale per i blocchi di rivestimento e i blocchi di tamponamento / aggregati alle loro spalle).

Ciò significa che i blocchi del nucleo sull’estremo NE erano più in alto di poco più di 1/ 4 di pollice delle pietre del rivestimento, ma questo eccesso sarebbe rapidamente diminuito verso Sud-Ovest, dove le cime del rivestimento di pietra, infine superavano di 1" i blocchi del nucleo.

I blocchi principali di questo livello stavano all’interno di un perimetro quadrato di 8.580" (715’ = 217,90 m).

6. Petrie ha stabilito che questo livello 6 saliva di 38" sul lato NE e 39,6" sul lato SW. Ancora una volta si tentava di riportare tutto a livello favorendo il lato SW. Sembrerebbe che i costruttori avessero fatto la faccia di pietra di lunghezza 49,5" per questo livello. La formula è 49,5" x sen 51,84° = 38,92123".

I blocchi principali di questo livello stavano all’interno di un perimetro quadrato, di lato 8.520" (710' = 216,40 m). La lunghezza della faccia inclinata ha ormai raggiunto 355,5" (9 m).

7. Petrie ha stabilito che questo livello 7 s’innalzava di 39,2" sul lato NE e 44,1" sul lato SW. Ora i livelli interni, ancora una volta, sono seriamente imprecisi e ci vorrà un ampio lavoro di riparazione per ristabilire la perfezione. Per ripristinare il livello di lavoro interno per i blocchi di base e dei materiali di riempimento, che formano un perimetro intorno, la lunghezza diagonale delle facce delle pietre di telaio deve essere 56". La formula è: 56" x sen 51,84° = 44,032". Ciò significa che la parte superiore del rivestimento in pietra al lato estremo NE stava incredibilmente a circa 5,47" più in alto dei blocchi verso l’interno del nucleo, e che il nucleo del lato SW stava 1/15 di pollice più in alto del rivestimento in pietra.

I blocchi del nucleo erano collocati all’interno di un perimetro quadrato dal lato di 8.460" (705’ = 214,90 m). L’altezza inclinata della faccia ha ormai raggiunto 411,5" (10,45 m).

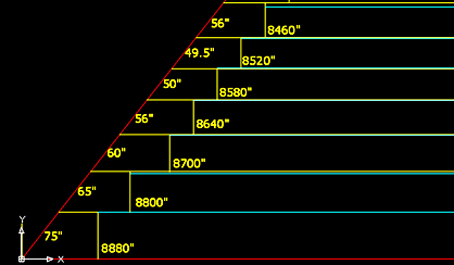
I primi sette corsi o livelli sono mostrati nella foto sopra. Le linee blu leggermente fuori di livello che vanno da una parte all’altra della piramide alla mostrano l’altezza di livello dei blocchi più interni del nucleo, misurata da Petrie, livello per livello. Da questa laboriosa rielaborazione in AutoCAD, diventa chiaro il motivo per i valori di aumento delle misure verticali dei blocchi, che prima sembrava inspiegabile. L’unica considerazione importante per gli architetti era la lunghezza della faccia finita inclinata, visibile, delle pietre dell’involucro, che doveva uguagliare un valore codificato. Si può tranquillamente ritenere che gli architetti della piramide non abbiano voluto utilizzare una qualsiasi frazione complessa su questa superficie esterna, ma che abbiano limitato l’uso delle frazioni di pollice a valori non inferiori al mezzo pollice. Fare altrimenti avrebbe aumentato enormemente il rischio di errori striscianti per i requisiti di "perfezione ottica" voluti, per le dimensioni dell’involucro di pietra.

Se gli scienziati antichi fossero stati in grado di ottenere materiali specializzati (flessibili), in modo tale da realizzare tubi flessibili come quelli moderni, avrebbero potuto realizzare una superficie piana a livello, con incrementi molto precisi, livello per livello, su tutta la sommità dell’involucro di pietra intorno alla piramide intera (mediante l’uso di un semplice dispositivo di livello ad acqua). Sappiamo che essi potevano produrre tubi di rame. In assenza di un teodolite per rilevare i livelli di quota, un moderno carpentiere, che traccia le fondamenta di una casa, può raggiungere livelli perfetti tutto intorno, con nient’altro che un tubo da giardino riempito d’acqua.

Abbiamo stabilito un punto di partenza. Alcuni critici potrebbero considerare questo necessario impegno come un esercizio troppo noioso, privo di ogni merito. Tuttavia, circa 130 anni fa Petrie si assunse personalmente la briga immensa di arrampicarsi su per un lato della Grande Piramide e giù per l’altro, per ottenere misurazioni doppie, ben precise, con il teodolite su ogni livello. Egli ci ha lasciato un corpo di informazioni degne di approfondimento, faticosamente acquisite, ancorché tradizionalmente trascurati. Se mai riusciremo a comprendere il progetto architettonico originale, le dimensioni previste per gli strati successivi di involucro di pietre, allora potremo applicare la trigonometria sul nucleo interno della Piramide, come è sopravvissuto, al fine di formulare una teoria razionale.

ARTICOLO ORIGINALE