Liutprand - Associazione Culturale

La tradizione antica

Pitagora, contemporaneo di Buddha e di Confucio, non lasciò documenti scritti, ma i teoremi raccolti dai suoi discepoli furono sistemati da Euclide, il quale inventò i termini “filosofia” (amore della saggezza) e “matematica” (ciò che riguarda la scienza).

Il teorema di Pitagora afferma che l’area del quadrato costruito sull’ipotenusa d’un triangolo rettangolo è uguale alla somma dei quadrati costruiti sui due cateti. Esso costituisce la base dell’uso diffuso della cordicella a nodi dei costruttori medievali.

Cantiere medievale.

La cordicella a nodi e la canna dei costruttori sono strumenti usati dai costruttori sin dall’antichità, da egizi, greci e romani, e poi lungo tutto il medioevo. Essi permettono di tradurre semplicemente le principali costruzioni geometriche in forme concrete, sul terreno e sul cantiere. Essa serve a tracciare linee rette, a riportare misure, a tracciare circonferenze.

Un disegno dal taccuino dell’architetto Villard de Honnecourt (sec. XIII).

La cordicella a nodi è suddivisa da nodi in intervalli regolari, di uguale misura. La più usata ha tredici nodi e dodici intervalli. L’unità di misura più frequente, tra un nodo e l’altro, è il braccio o cubito. Si usa ancor oggi per il tracciamento di angoli retti ed è chiamata anche “corda egiziana”, “corda pitagorica” o “corda dei Druidi”, perché si ritiene che il suo uso derivi da antiche conoscenze iniziatiche e perché concretizza gli studi di Pitagora sui triangoli rettangoli. Il suo uso permette di tracciare sul terreno gli angoli retti e altri elementi di un progetto, taluni con precisione geometrica e altri con un’approssimazione sufficiente per gli usi pratici. In particolare, la cordicella a dodici intervalli, oltre all’angolo retto derivato dal “triangolo pitagorico” di lati 3, 4 e 5, aiuta a tracciare: il triangolo equilatero col lato di 4 cubiti, il quadrato col lato di 3 cubiti; un rettangolo di lati 2 e 4 cubiti, una piramide e una circonferenza.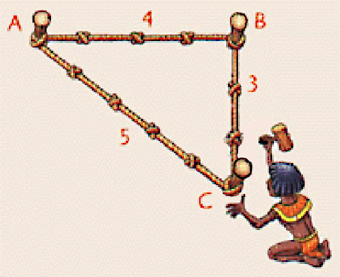

L’uso della corda pitagorica.

Il principio del triangolo 3, 4 e 5 è chiaro: sommando i quadrati dei due cateti si ha 9 + 16 = 25, che corrisponde al valore di 5 per l’ipotenusa. Gli angoli acuti di questo triangolo rettangolo misurano circa 36°52’ e 53°08’, e non 30° e 60°. Nel caso di angoli 30° – 60°, a un’ipotenusa che misuri 5 unità corrisponderebbero due cateti delle misure di 2,5 e 4,33 ca. Diverse cordicelle, aggiunte l’una all’altra, possono permettere di operare con un numero superiore di nodi. La cordicella a nodi permette di tracciare linee perpendicolari e parallele, grazie all’uso del triangolo pitagorico, e anche di realizzare elementi con lati in proporzione aurea Fi greco = (√5 + 1)/2 = 1,618034 ca.

Le unità di misura medievali (gotiche)

Secondo alcuni studiosi francesi d’architettura sacra, i costruttori medievali – in particolare le maestranze collegate ai monaci cistercensi – avevano elaborato un sistema di unità di misura basato sul rapporto modulare di Fi greco (1,618034 ca.).

Il piede generalmente usato nell’architettura gotica (conosciuto in Europa come piede parigino) misurava 144 linee, ossia 32,36 cm, ed era diverso dal piede romano, che rimase in uso in Italia sino alle costruzioni dell’epoca romanica.

La linea – o atomo, o grano – equivaleva alla dimensione del grano d’orzo: 0,2247 cm.

Un’unità di misura importante per l’architettura era il braccio o cubito, che i romani chiamavano “ulna”. Il cubito maggiormente utilizzato dai costruttori medievali, diffuso attraverso l’Europa dall’ordine cistercense, misurava 52,36 cm, ossia un piede parigino x 1,618.

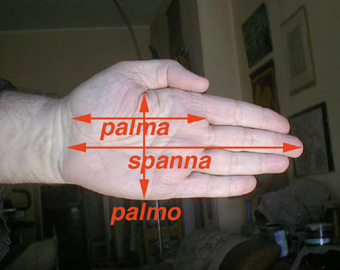
Le misure derivate dalla mano umana.

Si noti che il rapporto 1,6, oltre ad esprimere in modo approssimato il valore della sezione aurea, costituisce anche un valore approssimato di Pi greco / 2, ossia del rapporto tra la semi–circonferenza e il suo diametro. Tale caratteristica era utile tanto per realizzare le centine degli archi a tutto sesto, quanto per tracciare sul terreno i perimetri semicircolari delle absidi.

In effetti, più che non una continua e costante successione di unità di misura sulla base del “rapporto aureo”, appare più probabile – e più funzionale – l’uso nel mondo delle costruzioni di due sistemi di misura “paralleli”, nel quale alle principali unità di misura (diverse da quelle dei tessitori o di altri artigiani) corrispondeva un’altra “scala” o progressione di misure, corrispondenti alle prime moltiplicate per il rapporto aureo. All’interno di ciascuno dei due sistemi di misura “paralleli” la norma per passare da una misura a quella di ordine superiore doveva essere di ragione decimale (mentre gli altri artigiani usavano un fattore di moltiplicazione duodecimale, in modo da ottenere per ogni misura i sottomultipli /3 e /4). In tal modo, scegliendo ogni volta una misura in una scala (ad es. piede) ed una nell’altra (ad es. braccio), si otteneva tra le due il rapporto aureo. Un modo complesso, ma ben più efficace per concretizzare le geometrie di progetto di un sistema di unità di misura basato sull’unico moltiplicatore Fi greco. In tal caso, le conoscenze degli iniziati non si potevano limitare alle costruzioni di poligoni che oggi troviamo su un qualsiasi manuale di disegno, ma erano più sofisticate e conducevano a sapersi muovere a proprio agio nell’uso di due diverse scale di misurazione.

Altri autori, come Roland Bechmann, riconoscono l’esistenza nel Medioevo di una pluralità di sistemi di misura, che non furono mai ricondotti ad una matrice unica.

“Ogni maestro aveva il suo proprio gruppo e la sua propria tradizione, le sue abi¬tudini, i suoi strumenti e, in particolare, i suoi sistemi di misura. È stato possibile distin¬guere, infatti, nel corso della costruzione della cattedrale di Chartres, l’adozione di alme¬no otto sistemi di misura differenti. Ciò spiega le leggere differenze che si riscontrano anche in una stessa costruzione". (J. JAMES, Chartres: 1977-1978, Les constructeurs, 3 vol., Chartres, S.té Archéologique d’Eure et Loire, 1977, II, p. 21).

Si può immaginare che, quando il rappresentante del Capitolo dava le sue istruzioni e trasmetteva le direttive al maestro, quest’ultimo non potesse non fargli osservare che utilizzava le proprie unità di misura: “D’accordo! gli rispondeva allora il canonico, prendi il tuo piede!” È così che questa espressione avrebbe assunto il significato di "agire liberamente, secondo la propria discrezione".

(R. BECHMANN, Les racines des cathédrales, Paris, Payot, 1981 (tr. it.: Le radici delle cattedrali, Marietti, 1984 e Mondadori, 1989, p. 218).

La costruzione dei poligoni regolari

Le costruzioni di un triangolo equilatero, un quadrato, un esagono o un dodecagono inscritti in una circonferenza sono semplici a farsi sulla carta con un compasso e sul terreno con l’uso d’una semplice cordicella. Tali costruzioni sono ben note e ripetute su tutti i trattati elementari di disegno. Anche la costruzione del pentagono (e quindi del decagono) regolare non è difficile.

Una costruzione molto semplice e sufficientemente approssimata dell’eptagono regolare, con la cordicella a nodi, era quella di dividere in dieci parti il raggio della circonferenza e poi tracciare la corda perpendicolare al nono nodo, che corrisponde al lato dell’eptagono

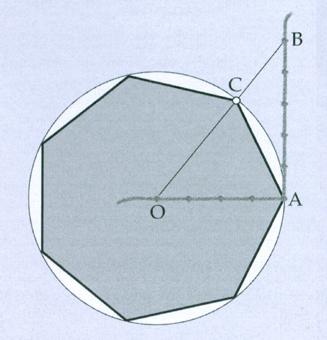
Una delle costruzioni dell’eptagono regolare.

Quanto all’ottagono inscritto, la cordicella permette una costruzione che si basa sul tracciato dell’esagono regolare e sulla forma a mandorla della vesica piscis (lato uguale al raggio della circonferenza). Centrando in G, con raggio uguale al raggio della circonferenza, si interseca la stessa in K e in L, che sono il secondo e l’ultimo vertice d’un ottagono inscritto, con i vertici disposti lungo i diametri ortogonali.

Un disegno dal taccuino dell’architetto Villard de Honnecourt (sec. XIII).

(cfr. A. ARECCHI, Spazi magici, Pavia, Liutprand, 1995).